String Matching
- The naive string-matching algorithm
- The Rabin-Karp algorithm
- String matching with finite automata
- The Knuth-Morris-Pratt algorithm
텍스트 \(T[1..n]\)
패턴 \(P[1..m]\)
\(\Sigma\) : 문자열에 사용되는 알파벳 집합
The naive string-matching algorithm
===================================
-
전처리 0
-
매칭시간 \(O((n-m+1)m)\)
가장간단하면서 일반적으로 생각할수있는 방법이다. 각 \(k\)마다 \(T[k]\)부터 \(T[k+m-1]\)까지 하나하나 \(P\)와 맞는지 확인하는것이다.
1
2
3
4
5
6
NAIVE-STRING-MATCHER (T,P)
n = T.length
m = P.length
for s = 0 to n-m
if(P[1..m] == T[s+1..s+m])
print ``Pattern occurs with shift s"
The Rabin-Karp algorithm
========================
-
전처리 \(\Theta(m)\)
-
매칭시간 \(O((n-m+1)m)\)
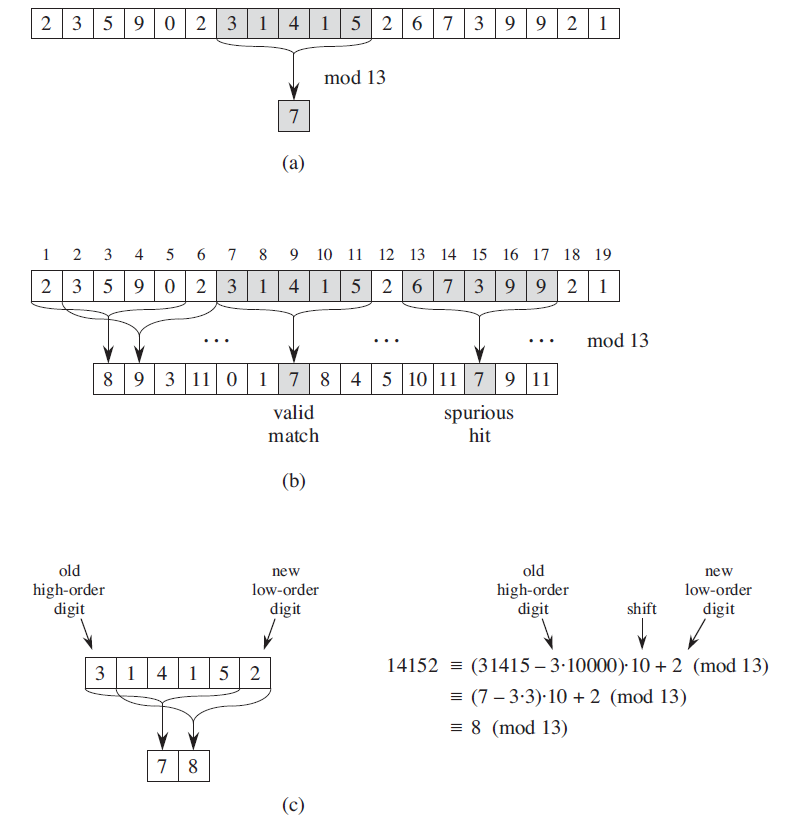
\(d = 10\), \(q = 13\)에 대한 라빈카프 알고리즘에 대한 수행을 나타낸다. (a)는 ``31415”에 대한 t가 7인모습 (b)는 숫자가 겹치지만 서로 다른 문자열에 대한것 (c)는 숫자비교를 끝낸후 다음 문자열에대한 변환을 나타낸 것이다.
수행시간을 개선하는 첫번째 아이디어는 문자를 숫자로 바꾸는것이다. \(111\)과 \(121\)이란 문자열을 비교하려면 첫번째방법인 각 자리별로 3번 비교해야하지만 숫자로 비교하는건 한번만 비교하면된다. 따라서 문자열을 숫자로 바꾸기위한 전처리 시간이 든다. 전처리는 \(P\)패턴만을 \(\Theta(m)\)동안 바꾸고 문자열 \(T\)는 비교와 동시에 처리한다.
그다음 문자열을 어떻게 숫자로 나타낼까를 고민해야하는데 이때 문자가 나타내는 언어의 총갯수에대한 진법에서 10진법으로 변환한다. 따라서 실제 알고리즘을 실행할때 언어의 총갯수 \(d\) \((|\Sigma|)\)를 인자로 넣어주어야한다. 이때 숫자로 바꿀때 너무 긴 문자열을 숫자로 바꿀시에 나타나는 오버플로우를 감안해, 적당한 값으로 나눌 \(q\)를 채용한다.그래서 그 나타낸 숫자가 매칭이 이루어졌을때 실제로 같은 문자열인지 검사하는 부분이 필요하다. 이 \(q\)는 일반적으로 \(dq\)가 컴퓨터 한워드에 들어가는 소수로 채용한다.
호너의 법칙(Horner’s law)을 사용해 다음의 수식으로 \(\Theta(m)\)시간에 패턴 \(P\)에대한 숫자 \(p\)를 전처리한다.
\[p = (dp+P[i]) \bmod q\]문자열 \(T[s+1..s+m]\)에 대한 숫자 \(t_s\)의 처리는 매칭과 직후에 계산 한다.
\[t_{s+1} = (d(t_s - T[s+1]h) + T[s+m+1]) \bmod q\]\(h = d^{m-1} \bmod q\)이다. 가장 앞의 \(T[s+1]\)을 \(h\)를 곱해 제거하고 왼쪽으로 시프트 후 \(T[s+m+1]\)를 더하는 방식이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
RABIN-KARP-MATCHER(T,P,d,q)
n = T.length
m = P.length
h = d^{m-1} mod q
p = 0
t_0 = 0
for( i = 1 to m)
p = (dp+P[i])mod q
t_0 = (dt_0 + T[i]) mod q
for s = 0 to n-m
if p == t_s
if P[1..m] == T[s+1..s+m]
print ``Pattern occurs with shift s"
if s < n - m
t_{s+1} = (d(t_s - T[s+1]h) + T[s+m+1]) mod q
이 방법은 초기보다는 확실하게 개선되었지만 여전히 완벽하게 일치하는지 확인하기 위해 하나하나 비교하는 방법을 사용한다. 이상적인 경우는 \((m-n+a)\)정도 돌겠지만 따라서 최악의 경우 매칭 시간이 \(O((n-m+1)m)\)이 된다.
String matching with finite automata
====================================
-
전처리 $$O(m \Sigma )$$ - 매칭시간 \(\Theta(n)\)
유한 오토마타
finite automaton은 다음과 같이 5개의 튜플로 구성된다.
-
\(Q\) : 유한 상태의 집합
-
\(q_0\) :시작 상태 (\(q_0 \in Q\))
-
\(A\) : 받아들이는 상태의 구분된 상태 (\(A \subset Q\))
-
\(\Sigma\) : 유한 입력 알파벳
-
\(\delta\) : \(Q \times \Sigma\)에서 \(Q\)로 매핑되는 전이 함수 \(M\)
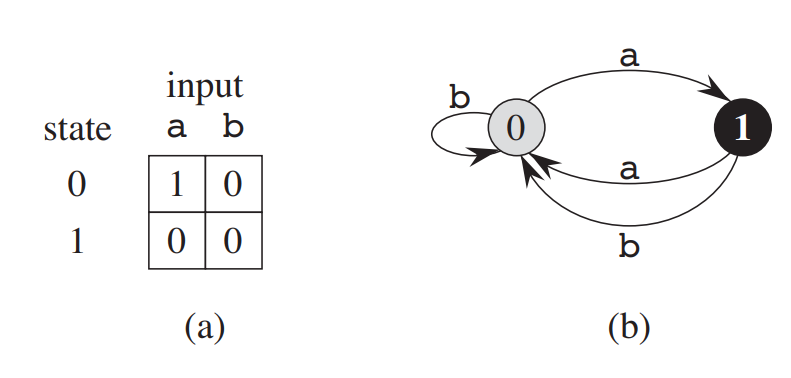
이런 그림을 예시로 들면
- \[Q = {0, 1}\]
- \[q_0 = 0\]
- \[A\]
- \[\Sigma = {a, b}\]
- \(\delta\)는 (a) 테이블을 나타낸다.
스트링 매칭 오토마타
- \[|\Sigma| = 3\]
- \[\Sigma = {a,b,c}\]
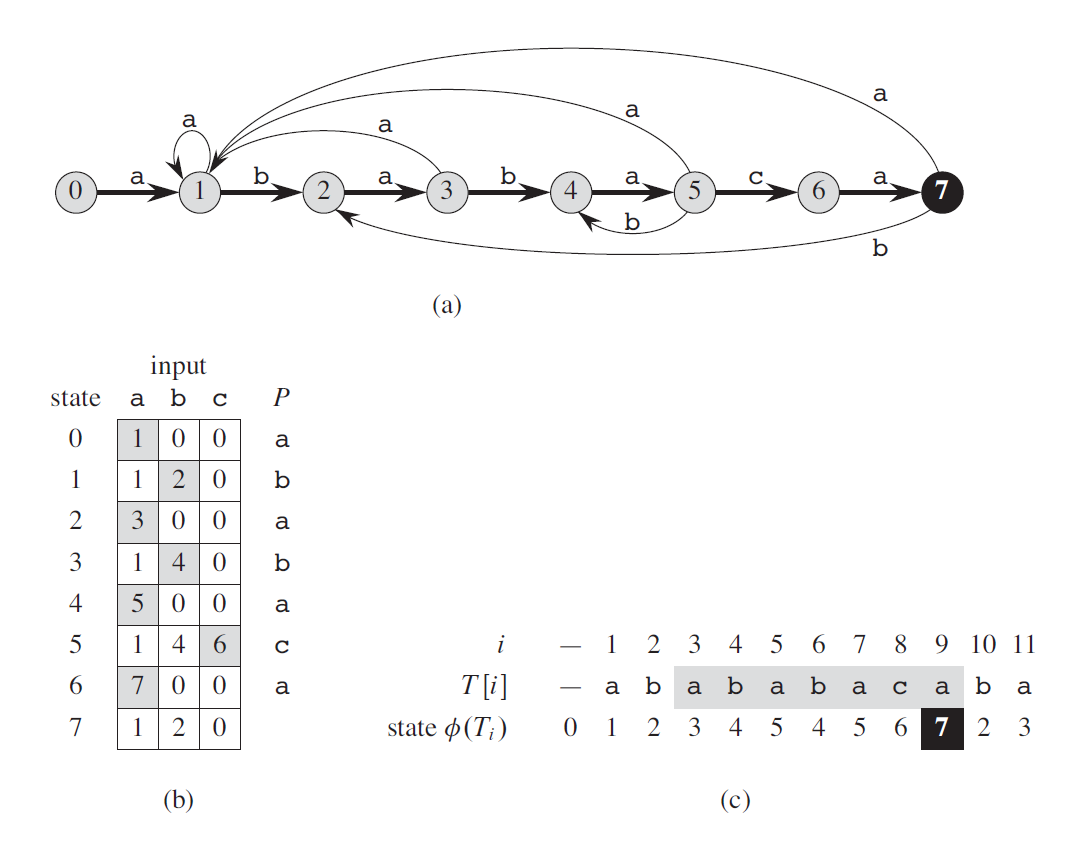
- \(m = 7\)에 대한 스트링 매칭 오토마타
- \[Q = {0, ... , m}\]
- \[q_0 = 0\]
- (a)패턴 \(P\)에 대한 상태 오토마타
- (b) \(\delta\) 상태표
- (c) 상태표에 따른 연산 예시
오토마타를 이용한 스트링 매칭은 전처리에 일치한 앞 문자열 상태에 따른 상태표 \(\delta\)를 구하고 이를 이용해 매칭을 하는것이다. 상태는 \(0,..,m\)까지 있다. 초기 시작 상태는 0이고(매칭되는 알파벳이 하나도 없는 상태) 매칭되는 알파벳갯수에따라 상태 넘버를 가진다.
매칭시에 문자열 \(T\)는 각 자리마다 상태를 가진다. 각 상태를 가지고 다음에 나오는 문자에 따라 상태를 변화시키고 상태가 \(m\)에 도달하면 매칭이 된것으로 본다.
상태표의 특징은 상태가 변할때 일치한 문자열이 가장 길게 일치하는 상태로 보내는 것이다. 가령 그림 (c)에서 \(T[5]\)에서 \(T[6]\)으로 넘어갈때 ``ababa“까지 일치했지만 ``b”가 나옴으로써 매칭이 실패하지만 뒤에나온 ``b“를 포함해 ``abab”까지가 일치하기에 상태가 4로 돌아간것을 볼수있다.
1
2
3
4
5
6
7
FINITE-AUTOMATON-MATCHER(T, delta , m)
n = T.length
q = 0
for i = 1 to n
q = d(q,T[i])
if q == m
print ``Pattern occurs with shift i-m"
상태표를 구하기위해서 다음과 같이 진행한다. 각 상태 \(q\) 마다 각 알파벳 \(a\)를 뽑는다. 현재 상태 \(q\)의 문자열 + ’a’가 임의의 상태 \(k\)를 끝에서 포함하는지 검사하고 다를시 \(k\)를 계속 낮춰간다.
1
2
3
4
5
6
7
8
9
10
COMPUTE-TRANSITION-FUNCTION(P, Sigma)
m = P.length
for q = 0 to m
for a in Sigma
k = min(m+1,q+2)
repeat
k = k - 1
until P_k ] P_q-a
d(q,a) = k
return d
다음의 전처리의 수행시간은 \(O(m^3 \Sigma)\)이다. 뒷절의 \(KMP\)방식을 차용해서 \(O(m \Sigma)\)로 개선할수있다.
라빈 카프보다 확실히 개선된 방안을 가졌으며 전처리에 문자열 \(T\)의 개입또한 없다. 그러나 위의 전처리 시간은 \(O(m^3 \Sigma)\)이며, 상태표의 공간 복잡도의 크기가 \(\Theta(m|\Sigma|)\)만큼 필요하다. 다음 절에서 이를 더 줄여볼것이다.
The Knuth-Morris-Pratt algorithm
================================
-
전처리 : \(O(m)\)
-
매칭시간 : \(\Theta(n)\)
흔히 KMP 알고리즘이라 부르는데 이 알고리즘은 처음의 가장 기본적인 비교방식을 개선했다고 볼 수 있다. 전처리를 통해 계산한 \(\pi[1..m]\) 배열을 사용하며, 매칭이 실패했을때, \(\pi\)배열을 사용한다.
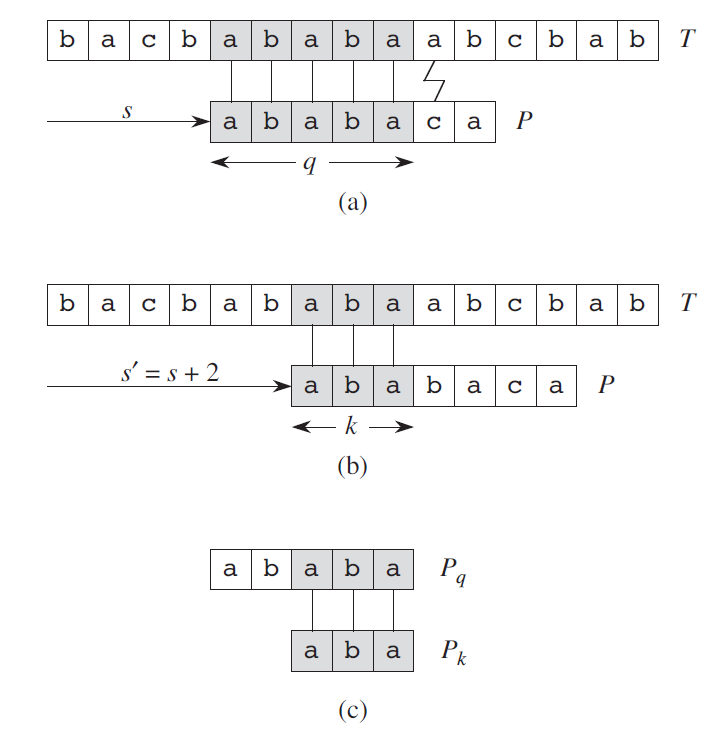
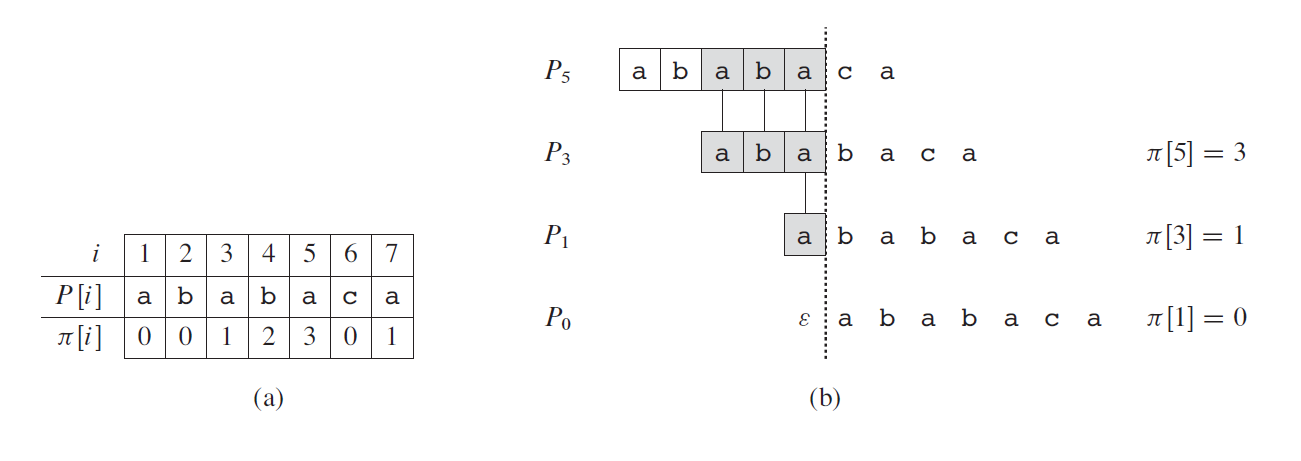
그림과 같이 ``ababaca“패턴을 문자열과 비교한다고 생각해보자. ``ababa”까지 맞지만 ’c’와 문자가 일치하지 않는다. 이때 앞의 문자열은 ``ababa“가 패턴이 일치하는것은 자명하다. 이때 ``ababa”에 가장 근접하고 일치하는 수가 적은 \(P\)의 패턴이 ``aba“임을 알수있는 배열 \(\pi[]\)를 이용해서 다시 비교하지 않아도 ``aba”까지 일치함을 알수있다.
(a)는 패턴 \(P\)와 전처리한 \(\pi[1..7]\) (b)는 \(P[5]\)에서 다음 문자가 매칭이 틀렸을때 그에 따른 \(\pi\)값과 되돌아가는 순서를 나타낸것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
KMP-MATCHER(T,P)
n = T.length
m = P:length
PI[] = COMPUTE-PREFIX-FUNCTION(P)
q = 0 // number of characters matched
for i = 1 to n // scan the text from left to right
while q>0 and P [q+1] != T[i]
q = PI[q] // next character does not match
if P [q+1] == T[i]
q = q + 1 // next character matches
if q == m // is all of P matched?
print "Pattern occurs with shift" i - m
q = PI[q]
COMPUTE-PREFIX-FUNCTION(P) /
m = P.length
let PI[1..m] be a new array
PI[1] = 0
k = 0
for q = 2 to m
while k>0 and P[k+1] != P[q]
k = P[k]
if P[k+1] == P[q]
k = k + 1
PI[q] = k
retunr PI
복잡도 분석 - COMPUTE-PREFIX-FUNCTION
\[\Theta(m)\]k의 값은 항상 q보다 작을 수 밖에 없다. 따라서 P[q]에 저장되는 값 또한 q보다 작을 수 밖에없다. k는 매 루프마다 최대 한번만 증가하며 최대 m - 1까지 커질 수 있다. while 문에서는 k가 작아지는 연산만을 한다. 하지만 k가 음수가 되지는 않는다. 이를 종합했을때 k가 최대로 상승할 수 있는 값은 m - 1이며 for전체에서 돌수있는 총 while문 횟수는 m - 1이 된다. 2m - 2로서 따라서 O(m)이 된다.