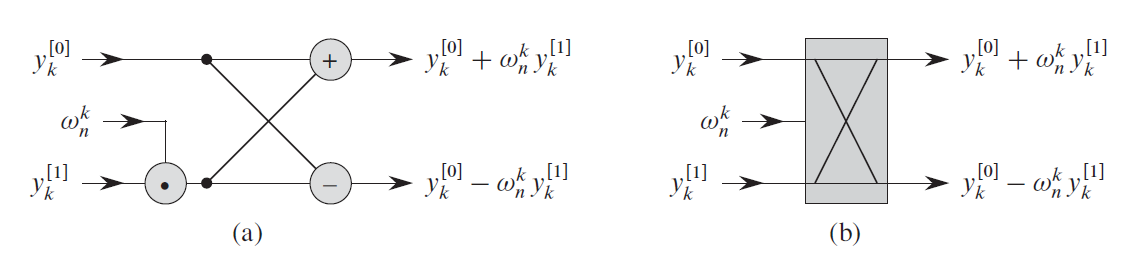개론

====

n차 다항식 \(A(x)\)를 예시로 들라고하면 대부분 이렇게 대답할것이다.

이는 컴퓨터상에서 크기가 \(n+1\)인 벡터(배열)에 \(\left\lbrace a_0,a_2, ... , a_n \right\rbrace\)으로 나타내도 \(A(x)\)를 확정지을 수 잇다. 이러한 표현 방식을 계수 표현(Coefficient representation)이라고 한다. 우리 일반적으로 사용하는 다항식을 나타내는 방식이라고 생각하면되는데. 이렇게 나타낸 다항식을 각각 곱하는 경우를 생각해보자. 일반적으로 우리는 종이에서 다음 다항식을 곱할때 이와같이 풀것이다.

2차나 3차의 경우는 한번에 쭉 풀수도있겠지만 n이 큰 경우일때는 어쩔수없이 \(A(x)\) 항하나에 \(B(x)\)를 곱해서 쭉 전개해서 풀것이다. 설명의 편의를 위해서 \(A(x)\)와 \(B(x)\)의 최고차항의 차수가 같다고 가정하고 내용을 진행할 것이고 전체 흐름에 따라 \(n\)의 의미가 중구난방적이다.

이를 직접 컴퓨터에서 계산한다고 생각해보자. 벡터 각요소에 벡터 각요소를 각각 모두 곱하기 때문에 시간복잡도는 \(O(n^2)\)이 될것이다. 이것이 우리가 일반적으로 생각하는 다항식 곱의 시간복잡도이다 이를 \(O(n \log n)\)으로 줄여 보는 것이 목표이다.

점값 표현

=========

중,고등학교를 나오면서 다음과 같은 문제를 푼적이 있을거라고 생각한다.

• 2차원 좌표상에서 \((1,0)\)과 \((6,8)\)을 지나는 직선의 방정식을 구하시오.

• 2차원 좌표상에서 \((1,0)\), \((6,8)\),\((-4,8)\) 을 지나는 다항함수를 구하시오.

간단한 연립방정식처럼 생각하면 최고차항의 차수가 \(n\)에 따라서 어떤 다항식을 지나는 \(n+1\)개 이상의 점의 좌표를 알고있으면 그 다항식을 특정할 수 있다. 컴퓨터상에서도 그대로 나타낼수 있다. \(\left\lbrace (x_1, y_1),(x_2, y_2), ... ,(x_n, y_n)\right\rbrace\)

이를 점값 표현(Point-value representation)이라고 한다. 점값 표현으로 이용할 특징은 같은 \(x\)좌표의 덧셈과 곱셈은 그냥 단순히 더하고 곱하면되는것이다. \(C(x) = A(x)B(x)\)에 대해서 \(A(x_k)*B(x_k) = C(x_k)\)가 된다. 따라서 점값표현으로 나타나있는 \(A(x)\)와 \(B(x)\)의 다항식 곱을 나타내기위해 \(O(n)\)의 시간만큼 걸린다. 하지만 점값표현 만으로 \(C(n)\)을 특정하기위해서는 \(2n-1\)만큼의 좌표쌍이 필요하다. 따라서 초기 \(A(x), B(x)\)의 좌표쌍 또한 각각 \(2x-1\)개 만큼 필요하다.

계수표현 점값표현 치환에 대한 고찰

==================================

앞에서 점값표현으로 나타냈을때 다항식의 곱이 간편하다는것을 알았다. 이제 계수표현으로 나타나있는 다항식을 점값표현으로 나타내고 이것의 역변환을 빠르게 할 생각을 하면된다.

1. \(x\)좌표를 임의로 잡고 하나씩 계산하는 경우이다.

   그럼 \(n+1\)개의 계수에 대해서 \(x\)가 \(x^n, ... , x\)를 구해서 계수를 각각 계산하는것은 \(n + \cdots + 1 = \dfrac{1}{2}n^2 + n\)만큼의 시간이 걸린다. 이때 \(x\)차수를 구하는 부분을 메모이제이션을 사용한다면 \(O(2n)\)만큼 걸린다.

2. 호어의 법칙(Horner’s rule) 특정값 \(x_0\)에 대해 점값표현을 가장 빠르게 구할방법은 연쇄적으로 계산을 하는것이다. \(A(x_0) = a_0 + x_0(a_1 + x_0(a_2+ \cdots + x_0(a_{n-2} + x_0(a_{n-1})) \cdots ))\) 위 방식에 비해서 추가적인 공간복잡도도 \(O(1)\)이며 메모리 접근도 적기때문에 훨씬 빠르다고 볼수있다. 하지만 \(n\)개의 점값표현을 구하기위해선 결국 \(O(n^2)\)만큼의 시간이 걸리기때문에 다항식을 쌩으로 곱하는것과 다를것이없다.

DFT와 FFT

=========

변환과 역변환에 \(O(n^2)\)으로 푸는 방법까지는 알았다. \(x\)점으로 복소수 근을 가지게 함으로써 변환에 \(O(n \log n)\)이 걸림을 보일 수 있다.

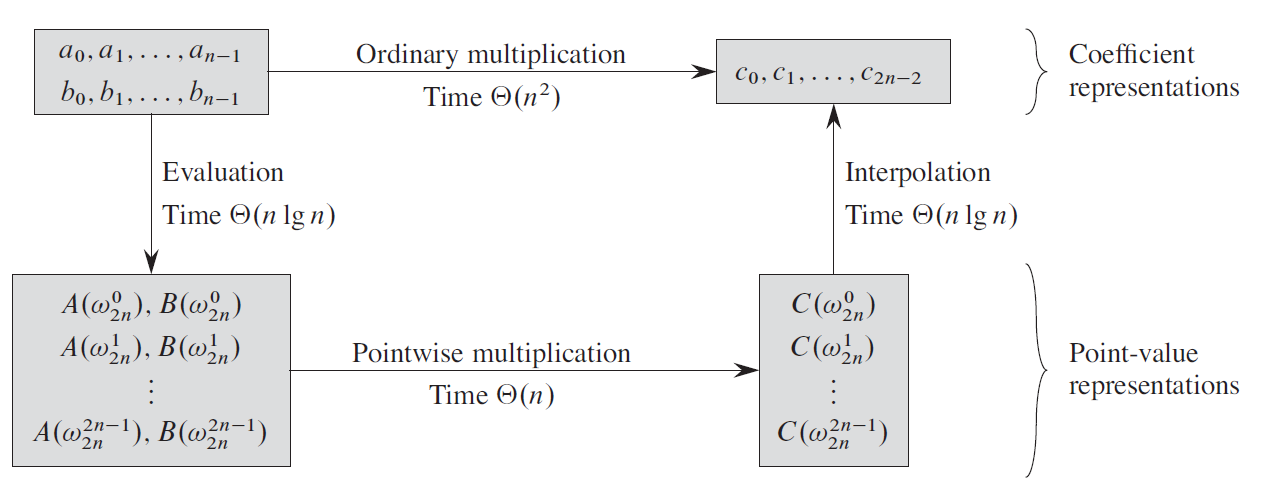
다항식곱의 전체 알고리즘 개형도

전체적인 순서는 이렇게된다.

1. \(A(x)\)와 \(B(x)\)에 \(n~2n\)까지의 차수의 계수를 0으로 놓아 다항식을 확장한다.
2. 각각 FFT를 적용하여 점값표현을 구한다.
3. 점별로 곱해 \(C(x)\)를 구한다.
4. 다시 FFT를 적용하여 \(C(x)\)를 계수형으로 바꾼다.

복소수

복소수는 오일러 방정식으로 부터 시작한다.

\(x = \pi\)를 넣으면 \(e^{i\pi} = -1\)이란 어디서 봤을 수도있는 식이다. 여기에 \(x = 2\pi\)를 넣으면 \(e^{2\pi i} = 1\)이란 식이 나온다. 이제 \(x = \frac{2\pi}{n}\)을 대입하여 \(\omega_n\)을 다음과 같이 정의하자.

\(\omega_n\)을 \(0\)부터 \(n-1\)까지 지수승 한 집합을 나타내자.

이는 순환 구조를 가진다. \(\omega_n ^0 = \omega_n^n = 1\)

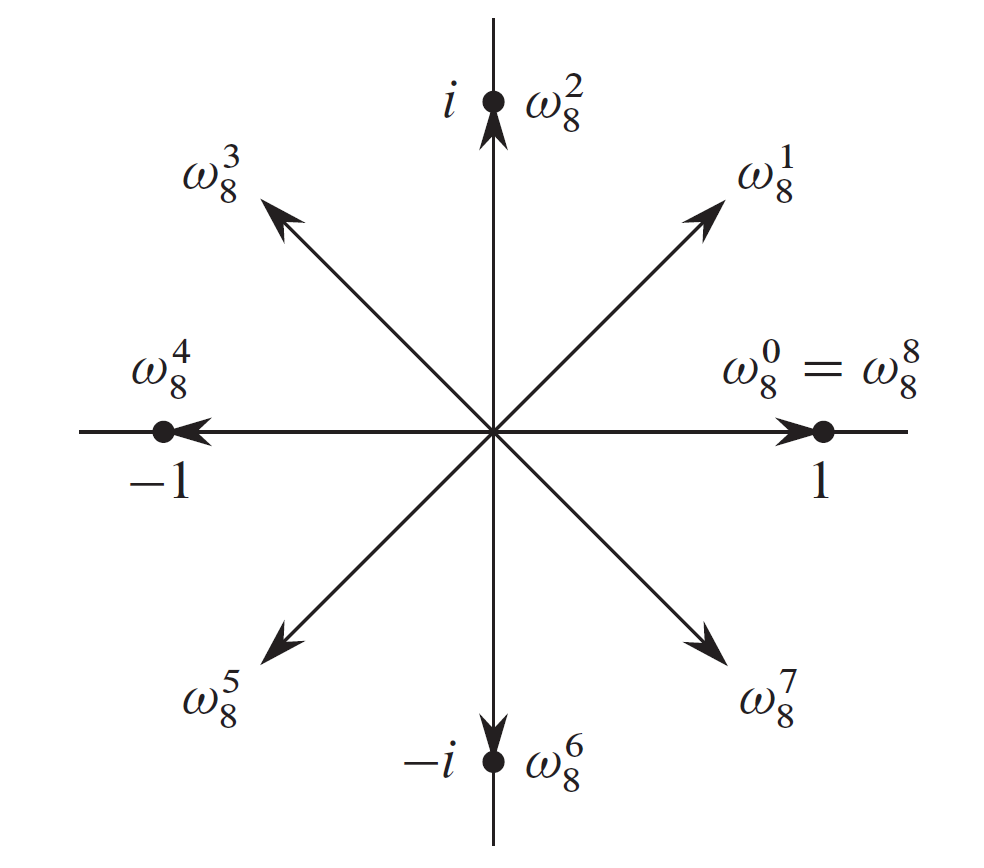
우리의 목적은 최고차항이 \(n-1\)인 다항식의 점값표현으로 쓸 \(x\)좌표로 다음의 집합을 채택하는것이다.

\(n = 8\)일때 8개의 좌표

DFT

계수형으로 나타나있는 \(A(x) = (a_0,a_1,...,a_n)\)로 다음 \(y = (y_0,y_1,...,y_n)\)벡터를 나타내는 것을 이산 푸리에 변환(DFT : Discrete Fourier Transform)이라한다.

쉽게 나타내면 계수표현으로 나타나 있는 \(A(x)\)를 n개의 집합에 대해(다항식이 결정되어있음) \(x\) 좌표가 각각 \(\left\lbrace \omega_n^0, \omega_n^1, \omega_n^2 , ... , \omega_n^{n-1}\right\rbrace\)인 \(y\)값의 집합이다.

FFT

DFT를 \(O(n \log n)\)에 구할수있는 알고리즘으로 고속 푸리에 변환(FFT :Fast Fourier Transform)이 있다.

FFT는 분할 정복(divide and conquer)기법을 사용한다.

\(A_{even}\)과 \(A_{odd}\)를 다음과 같이 정의하자.

• \[A_{even}(x) = a_0x^0 + a_2x^1 + a_4x^2 + \cdots + a_{n-2}x^{ \frac{n}{2}-1}\]
• \[A_{odd}(x) = a_1x^0 + a_3x^1 + a_5x^2 + \cdots + a_{n-1}x^{\frac{n}{2}-1}\]

\(A(x)\)를 다음과 같이 분할한다.

프로시저는 다음과 같다.

1. \(A_{even}\)과 \(A_{odd}\)로 나눈다.

2. \(A_{even}\)과 \(A_{odd}\)를 각각 재귀로 FFT한다.

3. \(A(x) = A_{even}(x^2) + xA_{odd}(x^2)\)에 따라서 계산한다. 이때 걸리는 복잡도는 \(O(n)\)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    RECURSIVE_FFT(a)
    n = length[a]
    if n = 1
        return a
    w_n = e ^{2 pi i / n}
    w = 1
    a_even = (a_0,a_2 , ..., a_n-2)
    a_odd = (a_1,a_3 , ..., a_n-1)

    y_even = RECURSIVE_FFT(a_even)
    y_odd = RECURSIVE_FFT(a_odd)
    for( k = 0 to n/2 -1 )
        y[k] = y_even[k] + w * y_odd[k]
        y[k+(n/2)] = y_even[k] - w * y_odd[k]
        w = w*w_n
    return y

다항식 \(n\) 개의 계수집합을 입력값으로 \(k = 1 ... n\)까지 \(x = \omega^k_n\) 에 대한 \(y\) 값의 좌표 집합을 반환하는 함수이다. 이 알고리즘은 2로 나눈 재귀를 두번부르고 후에 추가적인 \(O(n)\)연산이있다. \(T(n) = 2T\left(\dfrac{n}{2}\right) + \Theta(n) = \Theta(n \log n)\)

\(DFT^{-1}\) 역변환

=================

점값표현에 대해서 다음의 식이 성립이 한다.

\(DFT\)의 수행을 행렬식으로 나타냈을때, 다음의 행렬 곱셈 식을 이용했다.

이 행렬은 역행렬이 존재하며, 역변환에 대해서 다음의 식을 통해 원래의 값이 나온다.

n = 4 일때 수행 예시

====================

\(DFT\) 수행

계수 벡터 \(A = \left\lbrace a_0, a_1, a_2, a_3 \right\rbrace\)인 경우를 생각해보자. 이를 점값표현으로 변환, 역변환해 본다. 이에 대한 FFT 알고리즘 수행은 다음 과정을 거친다.

1. 분할: \(\left\lbrace a_0, a_2 \right\rbrace\), \(\left\lbrace a_1, a_3\right\rbrace\)

2. 분할: \(\left\lbrace a_0\right\rbrace , \left\lbrace a_2\right\rbrace , \left\lbrace a_1\right\rbrace , \left\lbrace a_3\right\rbrace\)

3. 결합: \(\left\lbrace a_0 + a_2, a_0 - a_2 \right\rbrace \left\lbrace a_1 + a_3, a_1 - a_3\right\rbrace\)

4. 결합: \(\left\lbrace (a_0 + a_1 + a_2 + a_3), (a_0 + \omega a_1 - a_2 -\omega a_3) , (a_0 - a_1 + a_2 - a_3), (a_0 - \omega a_1 - a_2 + \omega a_3) \right\rbrace\)

계수벡터에 \(1, \omega ,\omega^2 , \omega^3\)을 넣었을때의 결과와 동일하다.

\(DFT^{-1}\)수행

\(\omega^j = \left\lbrace \begin{array}{rl} 1 & ( j = 0, \theta = 0 ) \\ -i & ( j = -1, \theta = -\dfrac{1}{2}\pi) \\ -1 & ( j = -2, \theta = -\pi ) \\ i & ( j = -3, \theta = -\dfrac{3}{2}\pi ) \\ \end{array} \right.\)

\(e^{i\theta} = \cos \theta + i \sin \theta\)로 부터 다음식이 성립함을 알 수 있다. \(-\omega = \omega^{-1}\) [^1]

1. 분할: \(\left\lbrace y_0, y_2 \right\rbrace\), \(\left\lbrace y_1, y_3\right\rbrace\)

2. 분할: \(\left\lbrace y_0\right\rbrace , \left\lbrace y_2\right\rbrace , \left\lbrace y_1\right\rbrace , \left\lbrace y_3\right\rbrace\)

3. 결합: \(\left\lbrace y_0 + y_2, y_0 - y_2 \right\rbrace \left\lbrace y_1 + y_3, y_1 - y_3\right\rbrace\)

4. 결합: \(\left\lbrace (y_0 +y_1 + y_2 + y_3), (y_0 - \omega y_1 + y_2 +\omega y_3) , (y_0 - y_1 +y_2 - y_3), (y_0 + \omega y_1 - y_2 - \omega y_3) \right\rbrace\)

각\(y_n\)에 곱해지는 계수와 \(a_n\) 계수벡터를 풀어써서 행렬에 나타내면

여기서부터는 미완성

성능 개선

=========

첫번째로 반복계산되는것을 임시변수로 만들어서 계산을 줄이는 방법이 있다.

1
2
y[k] = y_even[k] + wy_odd[k]
y[k+(n/2)] = y_even[k] - wy_odd[k]

두번째로 루프풀기가 있다. fft의 루프풀기는 꽤 복잡하다. 분할정복기법에서 분할의 상태를 만들어놓고 반복문으로 conquer를 행한다. conquer시에 임시 배열로 할당되어 나뉘어져있던 짝수 홀수를 기존 하나의 큰 배열에 그대로 사용한다.(여기서 캐시성능 이득을 볼 수 있다.) 분할의 상태를 만들어 놓기위해 임의 위치 이동이 행해진다.

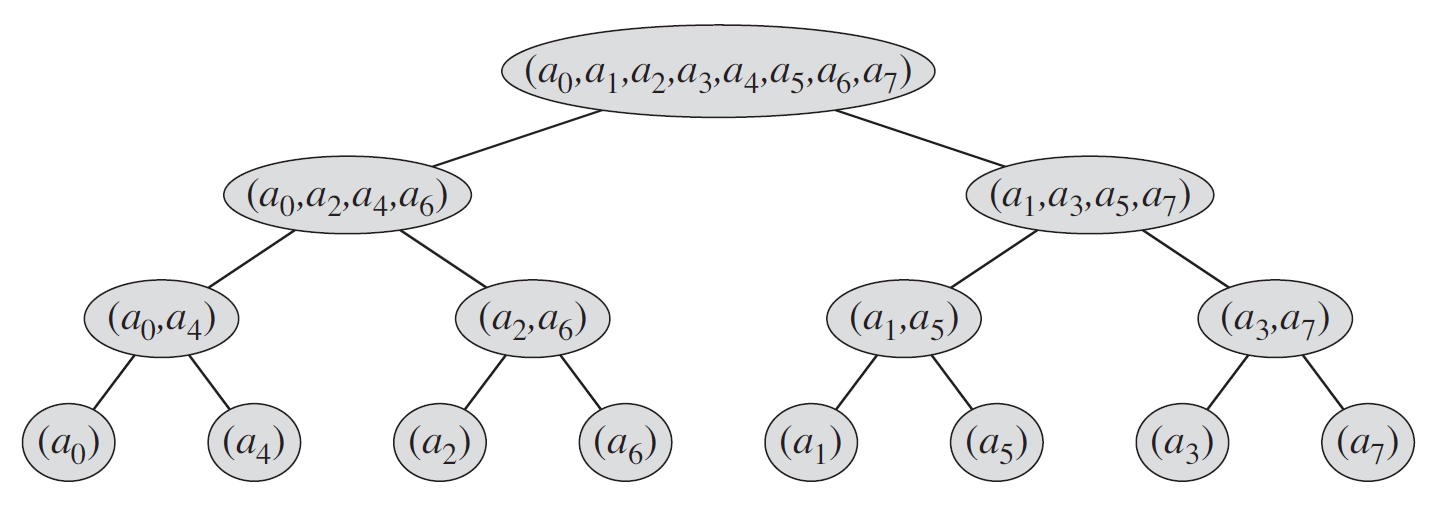
n = 8 일때,recursive시 분할되는 원소들. 루프풀기의 아이디어는 분할될때의 원소의 위치를 임의로 옮기는 것이다.

그 후에 각 위치에 맞는 원소들을 골라서 반복문으로 conqure처리를 한다.

Conqure 처리(butterfly diagram)

n = 8의 iterative-FFT 수행

이 때 옮겨지는 위치들은 비트 반전의 모습을 띄는데 각 원소들이 옮겨지는 위치들을 2진수로 나타내면 다음과 같다.

• 000 -> 000
• 001 -> 100
• 010 -> 010
• 011 -> 110
• 100 -> 001
• 101 -> 101
• 110 -> 011
• 111 -> 111

이를 이용해서 각 값에 맞는 배열 rev의 값을 쉽게 구할 수 있다.

    ITERATIVE-FFT(a)
        BIT-REVERSE-COPY(a, A)
        n = a.length // n is a power of 2
        for s = 1 to lg n
            m = 2^s
            w_m = e^{2pi i/m}
            for k = 0 to n-1 by m
                w = 1
                for j = 0 to m/2 -1
                    t = w A[k+ j + m /2]
                    u = A[k + j]
                    A[k + j] = u + t
                    A[k+ j + m /2] = u - t
                    w = w_m
        return A

    BIT-REVERSE-COPY(a, A)
        n = a.length
        for k = 0 to n - 1
            A[rev(k)] = a_k

마지막으로 parallel 알고리즘으로 바꾸는 방법이 있다. 작업단계는 \(\Theta(\lg n)\) 개이며 각 단계에서 \(2^{s-1}\)번 반복을 행하는 나비 집합이 \(n/2^s\) 개 존재한다. 따라서 해당 프로시저의 기대 수행시간은

이다

코드로 나타내기 C++

이 후의 실제 코드들은 온전히 혼자 짠것이 아닌 다음의 사이트 등에서 찾아보고 수정하여 짠것임을 알립니다.

• https://gratus907.com/93
• https://speakerdeck.com/wookayin/fast-fourier-transform-algorithm?slide=11
• https://koosaga.com/139
• https://cubelover.tistory.com/12
• https://casterian.net/archives/297
• https://justicehui.github.io/hard-algorithm/2019/09/04/FFT/
• https://blog.naver.com/kks227/221633584963
• https://algoshitpo.github.io/2020/05/20/fft-ntt/

알고리즘은 실제 코드로 짜기위해 두가지 문제를 해결해야한다.

1. 허수를 어떻게 표현하지

\(\omega\)를 어떻게 코드로 표현할지 난감했었다. 허수와 실수를 가지는 자료형 하나로 보고 계산시에 처리해주는것으로 충분하다. FFT전후에는 허수값이 남아있을지 언정 모든 프로시저가 실행되고난 후에는 허수값이 남지 않기때문에 허수자체를 표현해줄 필요가 없이 계수만 기억하고 있으면 된다. 그리고 n을 구해야하는것과 같거나 더 큰 2의 거듭제곱으로 잡는다. 넘어가는 계수는 0이기에 편하다.

참고: \(\cos\)은 우함수(y축 대칭) \(\sin\)은 기함수(원점대칭)이다.

C++에서는 complex라는 복소수 자료형을 자체적으로 지원해준다.

1. 오차

대부분의 널린 FFT코드가 PS문제에서 통과를 못하는 중대한 이유다. 실수 허수부분에 각각 삼각함수값을 써야하니 당연히 실수형 자료형을 써야한다. 하지만 당연히 실수형은 컴퓨터상에서 완벽하게 나타나는 값이 아니기에 계산이 많아질수록 오차가 굉장히 벌어지게 되어 계산결과 값이 틀리게된다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
typedef complex<long double> base;
constexpr double PI = 3.14159265358979323846;


; void fft(vector <base>& a, bool invert)
{
	const int n = a.size();
	for (int i = 1, j = 0; i < n; i++)
	{
		int bit = n >> 1;
		for (; j >= bit; bit >>= 1)
		{
			j -= bit;
		}
		j += bit;
		if (i < j)
		{
			swap(a[i], a[j]);
		}
	}
	for (int len = 2; len <= n; len <<= 1)
	{
		double ang = 2 * PI / len * (invert ? -1 : 1);
		base wlen(cos(ang), sin(ang));
		for (int i = 0; i < n; i += len)
		{
			base w(1);
			for (int j = 0; j < len / 2; j++)
			{
				base u = a[i + j];
				base v = a[i + j + len / 2] * w;
				a[i + j] = u + v;
				a[i + j + len / 2] = u - v;
				w *= wlen;
			}
		}
	}
	if (invert)
	{
		for (int i = 0; i < n; i++)
		{
			a[i] /= n;
		}
	}
}

void multiply(const vector<ll>& a, const vector<ll>& b, vector<ll>& res)
{
	vector <base> fa(a.begin(), a.end());
	vector<base> fb(b.begin(), b.end());
	int n = 1;
	while (n < a.size() + b.size())
	{
		n <<= 1;
	}
	fa.resize(n);
	fb.resize(n);
	fft(fa, false);
	fft(fb, false);
	for (int i = 0; i < n; i++)
	{
		fa[i] *= fb[i];
	}
	fft(fa, true);
	res.resize(n);
	for (int i = 0; i < n; i++)
	{
		res[i] = round(fa[i].real());
	}
}

NTT