1 알고리즘 기초 지식

시간복잡도 정의

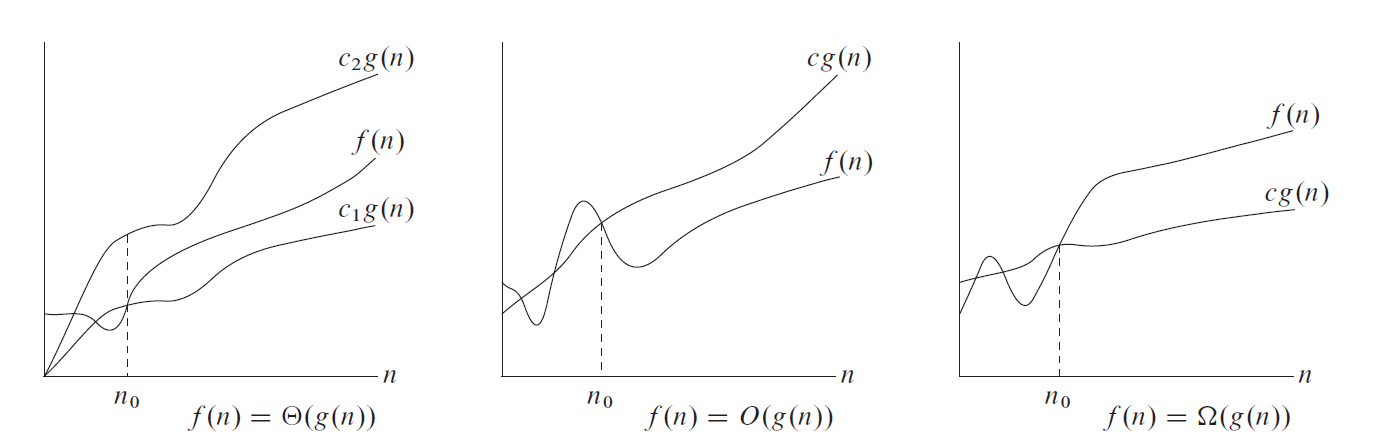
상한 big O $O$ :

함수 $\displaystyle f(n), g(n)$에 대해서 $0 \le f(n) \le cg(n) ( \forall n \leq n_0)$을 만족하는 $n_0$, 양의 상수 $c$가 존재할때 $f(n) = O(g(n))$이라한다.
하한 omega $\Omega$ :

함수 $f(n), g(n)$에 대해서 $0 \le cg(n) \le f(n) ( \forall n \leq n_0)$을 만족하는 $n_0$, 양의 상수 $c$가 존재할때 $f(n) = \Omega(g(n))$이라한다.
Theta $\Theta$ :

$\Theta(g(n))$일 필요충분 조건은 $f(n) = O(g(n))$이고 $f(n) = \Omega(g(n))$이 성립할때 이다.

시간복잡도 그래프 개형

예시 : $f(n) = n^2 + n + 3$ 의 시간복잡도

\[O(2^n)\]
\[O(n^3)\]
\[O(n^2)\]
\[\Omega(1)\]
\[\Omega(n)\]
\[\Omega(n^2)\]
\[\Theta(n^2)\]

Tip

$n_0$와 $c$는 내 마음대로 잡는다.
극한에서 함수의 대소관계로 생각하면 제일 편함!
계산하기 편한 함수를 임의로 잡아 계산한다.

예시) 조화 급수의 상한

\[f(x) = \sum_{k=1}^n \dfrac{1}{k}\] \[\begin{aligned} \sum_{k=1}^n \dfrac{1}{k} &\le \sum_{i=0}^{\lg n} \sum _{j=0}^{2^i-1} \dfrac{1}{2^i+j} \\ &\le \sum_{i=0}^{\lg n} \sum _{j=0}^{2^i-1} \dfrac{1}{2^i} \\ &=\sum_{i=0}^{\lg n} 1 \\ &\le \lg(n) + 1 \end{aligned}\] \[\therefore \sum_{k=1}^{n} \dfrac{1}{k} = O(\lg n)\]

적분을 이용한 상한,하한

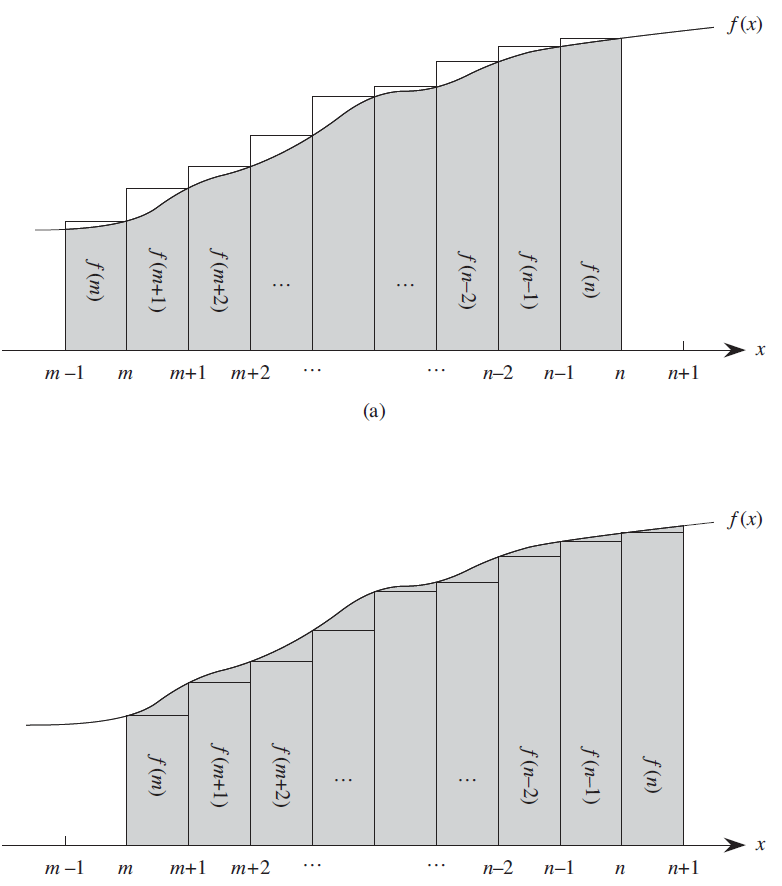
증가함수의 대소비교@reference1

\[\int_{m}^{n+1}f(x)dx \le \sum_{k=m}^n f(k) \le\int_{m-1}^{n}f(x)dx\]

단조 증가 함수 $f(k)$에 대해 다음이 성립함을 윗 그림 통해서 이해 할 수 있다. 감소함수는 이와 반대로 생각하면 쉽게 해당 부등식을 이해할 수 있다.

단조 감소 함수 $f(k)$에 대해서 다음이 성립한다

\[\int_{m-1}^{n}f(x)dx \le \sum_{k=m}^n f(k) \le \int_{m}^{n+1}f(x)dx\]

예시) 조화 급수의 상한과 하한

\[f(x) = \dfrac{1}{k}\]

하한

\[\sum_{k=2}^n \dfrac{1}{k}+1 \ge \int_{1}^{n}f(x)dx +1= \ln (n)+1 = \Omega(\ln n)\]

상한

\[\int_{1}^{n+1}f(x)dx =\ln (n+1) = O(\ln n) \ge \sum_{k=1}^n \dfrac{1}{k}\] \[\therefore \sum_{k=1}^n \dfrac{1}{k} = \Theta(\lg n)\]

스털링 근사 : $\lg(n!)$ 복잡도 구하기

\[\int_1^n \lg(k) dx +1 \le \sum_{k=2}^n \lg k + 1 \le \int_2^{n+1} \lg(k) dx +1\] \[n \lg(n) -n + 1 \le \lg(n!) \le (n+1)\lg(n+1) -(n+1) -(2\lg2 - 2)\] \[\begin{aligned} \therefore \lg(n!) = \Theta(n\lg n) \end{aligned}\]

실제 알고리즘 분석하기

INSERTION-SORT(A)
for j = 2 to A.length
    key = A[j]
    // Insert A[j] into the sorted sequence A[1 .. j - 1].
    i = j - 1
    while i > 0 and A[i] > key
        A[i + 1] = A[i]
        i = i - 1
    A[i + 1] = key

최악의 경우 시간 복잡도 : $\Theta(n^2)$
최선의 경우 시간 복잡도 : $\Theta(n)$
평균 시간 복잡도 : $\Theta(n^2)$
if에 의해서 정확하게 구하기 어렵다.
입력 자료의 상태에 따라 시간 복잡도는 바뀐다.
최악은 for문만을 가지고 단순 계산해도 무방.
ps에선 1초에 $10^9$(1억번)정도 계산한다고 생각하고 어림잡아 계산.

Posted 2021-07-13

clrs

eeeuns