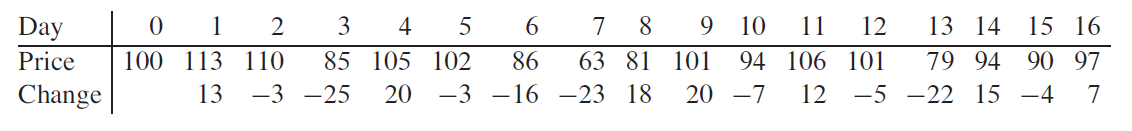• 1 알고리즘 기초 지식
• 2 분할정복(Divide and Conquer)
• 3 확률적 분석(Indicator random variables)

문제를 세가지 단계를 거치면서 재귀적으로 문제를 푼다.

1. 분할 : 현재의 문제와 동일하되 입력의 크기가 더 작은 다수의 부분 문제로 분할한다.

2. 정복 : 부분 문제를 재귀적으로 풀어서 정복. 부분 문제의 크기가 충분히 작으면 직접적인 방법으로 푼다.

3. 결합 : 부분 문제의 해를 결합해 원래 문제의 해가 되도록 만든다.

분할정복 예시

• 머지소트
• 최대부분 배열문제를 해결하는 알고리즘
• 퀵소트
• 행렬 곱
• FFT
• 카라추바 알고리즘

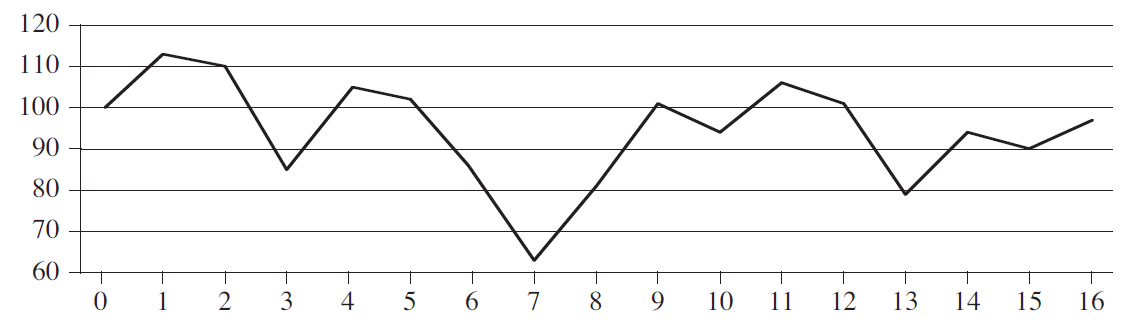
예시1. 최대 부분 배열문제(Maximum subarray problem)

• 배열값중 구간 끝값의 차가 가장 큰 구간 찾기

푸는법 1. 주먹구구

분할정복을 이용한 방법

• 인덱스 low… high 사이의 임의의 mid를 잡고 이 중 최대 부분 배열이 어디에 속하는지 생각해보자.
  1. low ,mid 사이
  2. mid high 사이
  3. mid를 걸치는 low high 사이

이것이 분할의 세가지 케이스이다.

분할정복을 이용한 방법

• 분할 : 일단 전체 길이를 반으로 쪼갠다.
• 정복 : 상수시간.
• 결합 : 걸쳐있는 경우 좌우 길이를 새로 구하고 각각의 길이를 리턴한뒤 비교한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    FIND-MAXIMUM-SUBARRAY(A, low, high)
    if high == low
        return (low, high,A[low]) // base case: only one element
    else mid = (low + high)/2 
        (left-low, left-high, left-sum) 
            = FIND-MAXIMUM-SUBARRAY(A, low, mid)
        (right-low, right-high, right-sum) 
            = FIND-MAXIMUM-SUBARRAY(A, mid + 1, high)
        (cross-low, cross-high, cross-sum) 
            = FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)

        if left-sum >= right-sum and left-sum >= cross-sum
            return (left-low, left-high, left-sum)
        elseif right-sum >= left-sum and right-sum >= cross-sum
            return (right-low, right-high, right-sum)
        else return (cross-low, cross-high, cross-sum)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    FIND-MAX-CROSSING-SUBARRAY(A, low, mid, high)
    left-sum = -inf
    sum = 0
    for i = mid downto low
        sum = sum + A[i]
        if sum > left-sum
            left-sum = sum
            max-left = i
            right-sum = -inf
    sum = 0
    for j = mid + 1 to high
        sum = sum + A[j ]
        if sum > right-sum
            right-sum = sum
            max-right = j
    return (max-left, max-right, left-sum + right-sum)

참고로 DP방법을 이용해 더 빠르게 풀 수 있다.

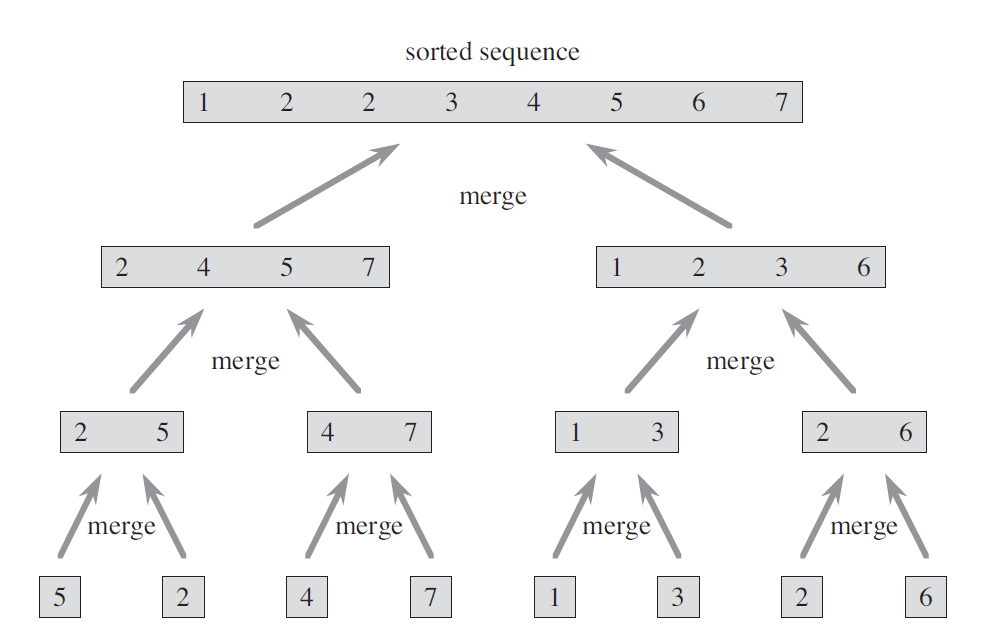
예시2. Merge Sort

• \[\Theta(n\lg n)\]
• 분할 : 정렬할 n개의 원소의 배열을 \(n/2\)개씩 부분 수열 두 개로 분할한다.
• 정복 : 두 부분 배열을 재귀적으로 정렬한다.
• 결합: 정렬된 두 개의 부분 배열을 병합해 정렬된 배열 하나로 만든다.

작동 이미지

1
2
3
4
5
6
    MERGE-SORT(A, p, r)
        if p < r
            q = (p + r)/2
            MERGE-SORT(A, p, q)
            MERGE-SORT(A, q + 1, r)
            MERGE(A, p, q, r)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
    MERGE(A, p, q, r)
        n1 = q - p + 1
        n2 = r - q
        let L[1...n1 + ] and R[1..n2 + 1] be new arrays
        for i = 1 to n1
            L[E] = A[p + i - 1]
        for j = 1 to n2
            R[j] = A[q + j]
        L[n1 + 1] = INF
        R[n2 + 1] = INF
        i = 1
        j = 1
        for k = p to r
            if L[i] <= R[j]
                A[k] = L[i]
                i = i + 1
        else 
            A[E] = R[j]
            j = j + 1

점화식

• 상수 \(c\)보다 작은 \(n\)에 대해 해를 직접 구하면 상수시간에 풀수있는경우. \(\Theta(1)\)
• 주어진 문제를 문제의 \(1/b\)인 \(a\)개의 문제로 분할 하는경우 : \(aT(n/b)\)
• 분할 : \(D(n)\)
• 결합 : \(C(n)\)

예시 : Merge sort 점화식

• 분할 : \(D(n) = \Theta(1)\)
• 정복 : \(2T(n/2)\)

• 결합 : \(C(n) = \Theta(n)\)

  \[T(n) = \begin{cases} \Theta(1) (\mbox{if } n = 1)\\ 2T(n/2) + \Theta(n) (\mbox{if } n > 1) \end{cases}\]

점화식 풀이법

1. 재귀 트리 방법(recursion tree method)
2. 치환법(substitution method)
3. 마스터 방법(master method)

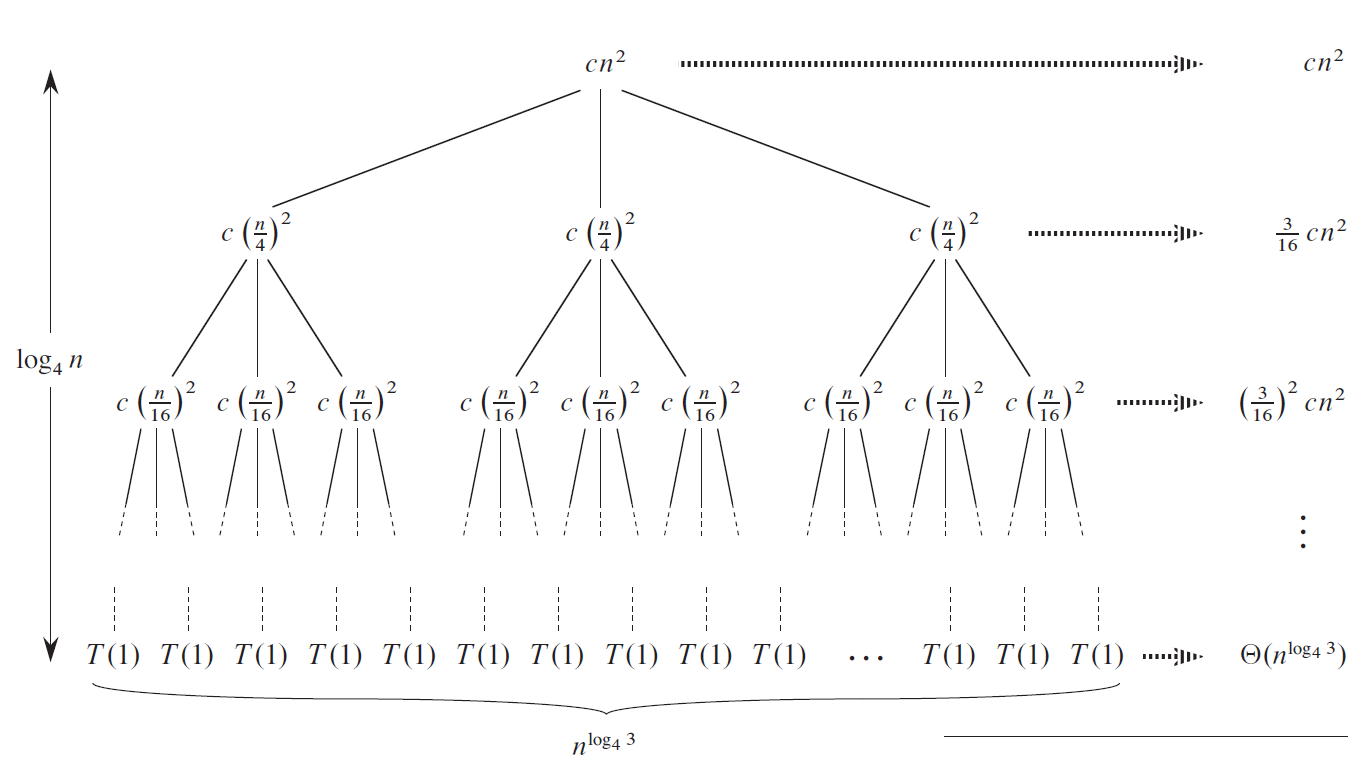
재귀 트리 방법

재귀 트리 방법 \(\Theta(n \lg n)\)

예시

풀이 \(\begin{aligned} T(n) &= \sum_{i=0}^{\log_4 n-1} \left( \dfrac{3}{16} \right) ^i cn^2 + \Theta(n^{\log_4 3}) \\ &< \sum_{i=0}^{\infty} \left( \dfrac{3}{16} \right)^i cn^2 + \Theta(n^{\log_4 3}) \\ &= \dfrac{1}{1-(3/16)}cn^2 + \Theta(n^{\log_4 3})\\ &= O(n^2) \end{aligned}\)

치환법

• 해의 모양을 추측한다.
• 상수들의 값을 찾아내기 위해 수학적 귀납법을 사용하고 제대로 동작함을 보인다.

예시 1.

• \(T(n) \le cn \lg n\) 이라고 추측

예시 2.

\(T(n) = O(n)\)이라고 추측

• \(T(n) \le cn\) X

• \(cn\)보다 좀더 작은 값을 추측할것.

  \[T(n) = 2T(n/2) + 1\]
• \(T(n) \le cn - d\)이라고 추측 \(\begin{aligned} T(n) &\le 2c(n/2)-d +1 \\ &= cn -2d + 1 \\ &\le cn - d \end{aligned}\)

마스터 정리

\(a(\ge 1)\)와 \(b(> 1)\)가 상수고 \(f(n))\)이 양의 함수라 하고, 음이 아닌 정수에 대해 \(T(n)\)이 다음 점화식에 의해 정의된다고 하자.

여기서 \(n/b\)는 \(\lfloor n/b \rfloor \lceil n/b \rceil\)를 뜻한다. 이때 \(T(n)\)의 점근적 한계는 다음과 같다.

1. 상수 \(\epsilon(>0)\)에 대해 \(f(n) = O(n^{\log_b a-\epsilon})\)이면, \(T(n) = \Theta(n^{\log_b a})\)이다.
2. \(f(n) = \Theta(n^{\log_b a})\)이면, \(T(n) = \Theta(n^{\log_b a} \lg n)\)이다.
3. 상수 \(c(<1)\)와 충분히 큰 모든 \(n\)에 대해 \(af(n/b) \le cf(n)\)이면, \(T(n) = \Theta(f(n))\)이다.

예시 1

• \[a = 9\]
• \[b = 3\]
• \[f(n) = n = O(n ^{\log _3 9 - \epsilon})\]
• case 1 : \(\Theta(n^2)\)

예시 2

• \[a = 1\]
• \[b = 3/2\]
• \[f(n) = 1 = \Theta(n ^{\log _{3/2}1}) = \Theta(1)\]
• case 2 \(\Theta(\lg n)\)

예시 3

• \[a = 3\]
• \[b = 4\]
• \(c = 3/4\)일 때 \(af(n/b) = 3(n/4) \lg(n/4) \le (3/4)n \lg n = cf(n)\)
• case 3 \(\Theta(nlg n)\)

예시 : 스트라센 알고리즘

\(T(n) = 7T(n/2) + \Theta(n^2)\) $$

• \[a = 7\]
• \[b = 2\]
• \[f(n) = n^2 = O(n ^{\log _2 7 - \epsilon})\]
• case 1 \(\therefore \Theta(n^{lg 7})\)

적용할 수 없는 점화식

• \[a = 2\]
• \[b = 2\]
• \(af(n/b) = 2(n/2) \lg(n/2) \le (3/4)n \lg n = cf(n)\) 인 \(c\)를 잡을 수 없음.
• case 3 X
• ???
• \(f(n)\)이 \(n^{\log_b a}\)보다 다항식적으로 크지않다면 구할 수 없음.